Didattica Matematica
- Dettagli
- Scritto da Alfonso D'Ambrosio
- Categoria: Didattica Matematica
- Visite: 9992
Buongiorno,
con questo articolo non solo voglio farvi gli auguri di Buon Anno Nuovo, ma anche raccontarvi un sogno, un sogno che si chiama Natura.
In matematica un frattale è sostanzialmente un oggetto che, se ingrandito, conserva le stesse proprietà di omogeneità ed isotropia.
Cerchiamo di spiegarlo più semplicemente: se ho una conchiglia e la ingrandisco, vedrò altre conchiglie uguali a quella iniziali e così via.
Oggetti simili li ritroviamo in casi comuni come la neve, i rami degli alberi (es. l’abete), le coste della Scandinavia, nei broccoli, nei profili delle montagne.

- Dettagli
- Scritto da Redazione PSN
- Categoria: Didattica Matematica
- Visite: 7827
 Un equivoco logico-matematico legato alla "legge dei grandi numeri" è capace di generare convinzioni palesemente sbagliate portando le persone con maggiore propensione al gioco a perdere, a causa di queste convinzioni, tempo e soprattutto molto denaro tanto da credere che esista la formula vincente per sbancare il lotto, il totocalcio, la roulette sfociando in vizio morboso del gioco.
Un equivoco logico-matematico legato alla "legge dei grandi numeri" è capace di generare convinzioni palesemente sbagliate portando le persone con maggiore propensione al gioco a perdere, a causa di queste convinzioni, tempo e soprattutto molto denaro tanto da credere che esista la formula vincente per sbancare il lotto, il totocalcio, la roulette sfociando in vizio morboso del gioco.
Sul tema proponiamo il pezzo scritto dal matematico e giornalista Giulio Simeone che ha affrontato la questione mettendo in luce le false credenze e convinzioni sulla legge dei grandi numeri e dimostrando la dipendenza del vizio del gioco con esse. Di seguito riportiamo il testo dell'articolo postato sul suo blog:
La famosa Legge dei grandi numeri viene invocata piuttosto di frequente nel linguaggio comune: peccato che abbastanza di frequente venga citata a sproposito, instillando nelle persone delle convinzioni sbagliate.
“Il Barcellona ha vinto nove partite consecutive, quindi per la legge dei grandi numeri è probabile che questa domenica perda”; “Sulla ruota di Venezia da tre anni non esce il 56, quindi lo gioco, per la legge dei grandi numerici sono buone probabilità che esca”; “Ieri c’è stato un incidente fatale sulla Tangenziale Est, quindi oggi ci posso passare tranquillamente, per la legge dei grandi numeri è quasi impossibile che se ne verifichi un altro”. Tutto sbagliato !
- Dettagli
- Scritto da Alfonso D'Ambrosio
- Categoria: Didattica Matematica
- Visite: 7384
Buongiorno,
quante potenzialità offre Scratch per la Matematica?
Tantissime....eppure il suo uso per questa disciplina è limitato alle "solite" cose
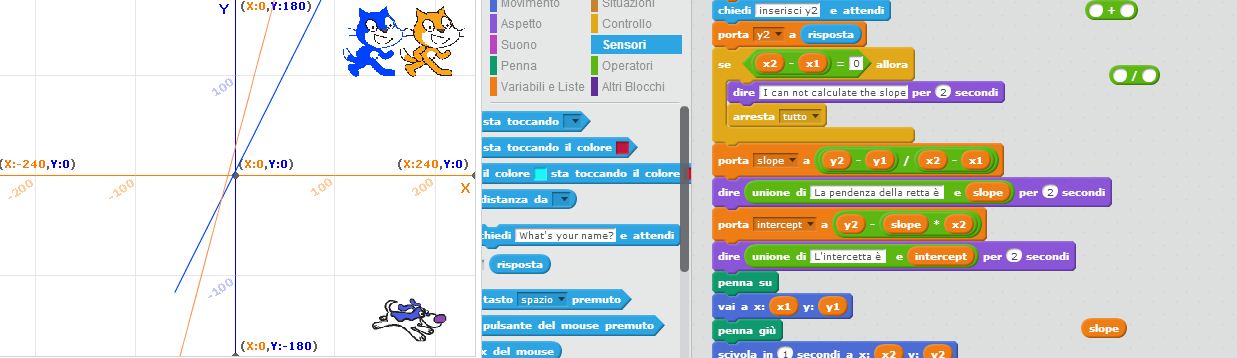
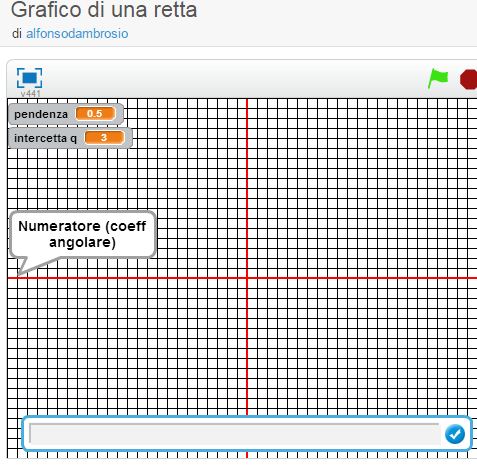
Perchè non fare coding anche creando un programma che ti permette di disegnare e determinare i parametri di una retta in un sistema di riferimento cartesiano?
Troppo complesso?
Ecco che interviene Scratch
Due semplici programmi, remixabili, con cui poter fare tutto questo ed anche confrontare grafici di rette con diverso coefficiente angolare ed intercetta per poter costruire un problem solving e problem coding sulle proprietà delle rette.
Qui i due programmi
https://scratch.mit.edu/projects/87074931/
https://scratch.mit.edu/projects/87076706/
Buon lavoro!
Per dubbi e suggerimenti scrivetemi ad Questo indirizzo email è protetto dagli spambots. È necessario abilitare JavaScript per vederlo.
- Dettagli
- Scritto da Alfonso D'Ambrosio
- Categoria: Didattica Matematica
- Visite: 8105
Chi ha detto che Scratch è un "gioco da ragazzi"?
Eccovi un semplice algoritmo per calcolare il numero di Nepero
Questo fantomatico numero di cui poco si dice ma tanti esercizi si fanno alle Superiori.

Con Scratch non è banalissimo risolvere l'algoritmo perchè non è immediato nè calcolare il fattoriale nè la potenza , infatti nei progetti ad oggi non era disponibile nessuno script che calcolasse il numero e di Nepero.
- Dettagli
- Scritto da Alfonso D'Ambrosio
- Categoria: Didattica Matematica
- Visite: 11158
Buongiorno,
chiunque mi conosce, sa quanto adoro Scratch e tutte le potenzialità che intravedo in esso.
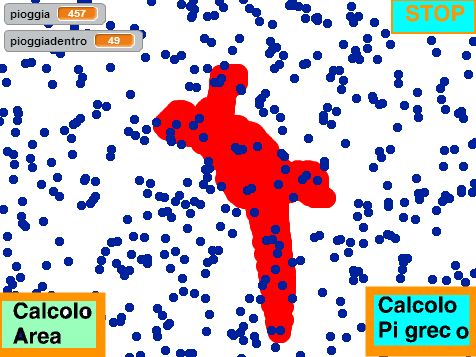
In questi giorni parlavo con il collega Alessandro Bencivenni sulla possibilità di misurare l’area di una generica figura. Quale modo migliore per farlo con Scratch?
L’attività proposta è spendibile sia durante le ore di lezione di Matematica, Fisica o informatica e nella Scuola Secondaria di I e di II grado.
Offre la possibilità di imparare ad utilizzare il coding , ma anche a programmare confrontandosi con un modello matematico non banale, ma potente ed affascinante (cerco di semplificare…ma se volete saperne di più cercate in rete le tags!).
- Dettagli
- Scritto da Alfonso D'Ambrosio
- Categoria: Didattica Matematica
- Visite: 10391
 Buongiorno, concludiamo il percorso sulle equazioni di primo grado, proponendo una analisi critica (secondo le più recenti metodologie di ricerca didattica) di alcuni esercizi proposti nei due articoli precedenti!
Buongiorno, concludiamo il percorso sulle equazioni di primo grado, proponendo una analisi critica (secondo le più recenti metodologie di ricerca didattica) di alcuni esercizi proposti nei due articoli precedenti!
Il presente lavoro si inserisce all'interno di un percorso critico, che fa uso di strumenti e metologie di ricerca didattica, sottolineo che noi insegnanti siamo i primi professionisti della scuola e spetta soprattutto a noi proporre attività innovative, un percorso non viene mai dall'alto, ma va sempre calato in relazione al contesto classe.
- Dettagli
- Scritto da Alfonso D'Ambrosio
- Categoria: Didattica Matematica
- Visite: 9412
 Buongiorno continuiamo oggi con la seconda parte sul percorso delle equazioni di primo grado. Le equazioni in generale sono un argomento fondamentale per la matematica e soprattutto per i nostri studenti. Come presentarle? Come affrontare i diversi approcci? Come può aiutarci una semplice programmazione al pc?
Buongiorno continuiamo oggi con la seconda parte sul percorso delle equazioni di primo grado. Le equazioni in generale sono un argomento fondamentale per la matematica e soprattutto per i nostri studenti. Come presentarle? Come affrontare i diversi approcci? Come può aiutarci una semplice programmazione al pc?
Continuiamo il nostro percorso di riflessione critica sulle equazioni di primo grado.
Buona lettura.
- Dettagli
- Scritto da Alfonso D'Ambrosio
- Categoria: Didattica Matematica
- Visite: 39671

Esiste un modo diverso di proporre le equazioni di primo grado, oltre alla solita introduzione algebrica? E' da preferire un metodo iconico o mostrare le equivalenze con la bilancia? e quanto può aiutarci l'informatica?
Perchè proporre certi esercizi/problemi piuttosto che altri? A queste ed altre domande cercherò di dare una risposta!
- Dettagli
- Scritto da Antonio Guerriero
- Categoria: Didattica Matematica
- Visite: 6000
La trasmissione Report di Milena Gabanelli, nella puntata "Startup Stories", dedicata alle esperienze tecnologiche più interessanti messe in campo nel nostro paese, ha documentato la didattica innovativa di "Matematica Sociale" adottata dall'Istituto "Virgilio 4" di Scampia dove la matematica si impara facendo la spesa o correndo in palestra per capire la differenza tra perimetro e superficie di una forma. Dove gli studenti sono chiamati a calarsi nei panni di insegnanti per introdurre i bimbi della scuola dell'infanzia, ai concetti di numeri e insiemi, alle operazioni e alla geometria: senza neanche una tabellina, ma con oggetti, animali e cose da comprare.
- Dettagli
- Scritto da Alfonso D'Ambrosio
- Categoria: Didattica Matematica
- Visite: 7340
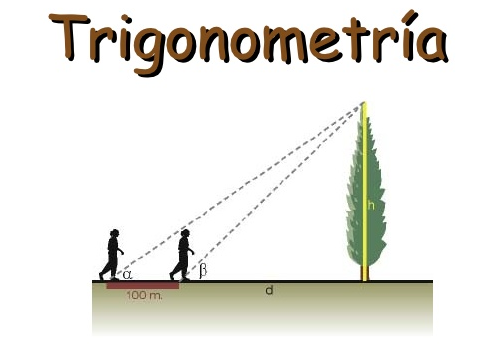
Buongiorno, terminiamo con oggi l'articolo "sperimentale" sulle funzioni goniometriche. Ricordiamo che la domanda a cui vogliamo rispondere è: come misurare l'altezza di un oggetto senza poterlo raggiungere?
La trigonometria risponde a questa domanda!
In questa fase i ragazzi costruiscono un semplice strumento per la misura dell'altezza di un corpo.
Gli strumenti sono stati realizzati in classe, utilizzando materiali di riciclo: tubo rotolo carta igienica ad uso puntatore (o in sostituzione un laser, incastrato sull'alta di legno superiore con dei chiodi), due aste di legno (o di pvc), un goniometro. Le due aste di legno sono state incernierate usando un cardine.

- Dettagli
- Scritto da Alfonso D'Ambrosio
- Categoria: Didattica Matematica
- Visite: 11284
Buongiorno, continuiamo con il presentarvi l'attività laboratoriale di matematica sulle funzioni goniometriche. L'attività vuole rispondere a domande quali: come misurare l'altezza di una torre o di un palazzo senza poter salire sulla sua sommità? come misurare la distanza tra due punti non direttamente raggiungibili?
La trigonometria affascina gli studenti, ma viene spesso presentata secondo un approccio molto teorico. I ragazzi non sempre colgono la potenza delle funzioni goniometriche nella risoluzione di problemi geometrici. E' per questo che tale attività viene presentata subito, fin dalla prima lezione sull'argomento. Non vengono presentati i concetti di radiante, seno coseno etc. ma vengono costruiti i concetti partendo dagli esperimenti.
- Dettagli
- Scritto da Alfonso D'Ambrosio
- Categoria: Didattica Matematica
- Visite: 13916
E' possibile fare matematica utilizzando esperienze di laboratorio, intendendo per esperienze di laboratorio esperimenti reali, non simulati ?
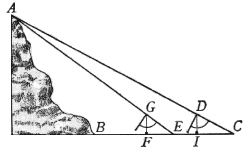
Il collega di estimo e topografia mi ha chiesto di anticipare l'attività sulla goniometria, in quanto i ragazzi utilizzano le funzioni goniometriche per misure reali di distanze. In questo articolo viene presentata una unità didattica così come è stata svolta quest'anno nella mia classe 3 indirizzo tecnico agrario. Il tentativo è quello di trasferire le conoscenze e competenze del laboratorio povero di fisica a quello di matematica, costruendo una didattica sulle competenze !
Pagina 1 di 2