Buongiorno,
riprende la rubrica di Laboratorio povero di Fisica e concludiamo l’anno descrivendo la seguente attività: la proporzionalità diretta ed inversa.
Setting didattico
Con i ragazzi (di prima Liceo Scientifico e terza Liceo Scienze umane) è stato discusso il concetto di proporzionalità diretta ed inversa. Da una prima indagine iniziale emerge che il concetto più frequente sulla proporzionalità direttainversa è:
All’aumentare di una grandezza , aumenta anche l’altra.
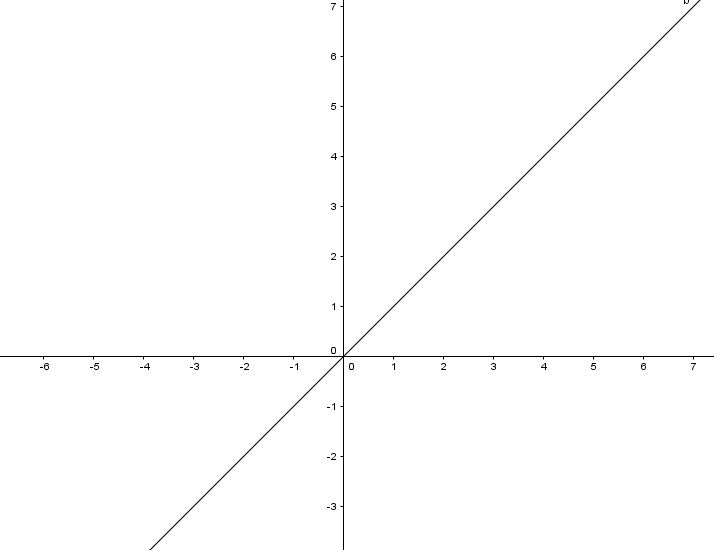
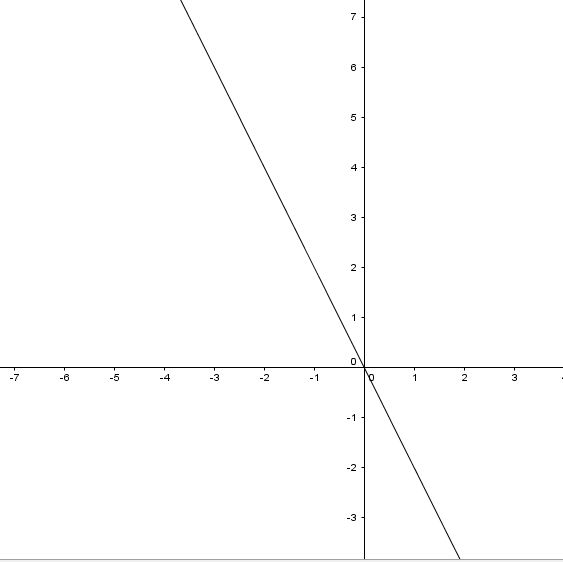
In tal senso le figure seguenti per gli studenti rappresentano dei buoni esempi di proporzionalità diretta.
Iscriviti alla nostra Fan page
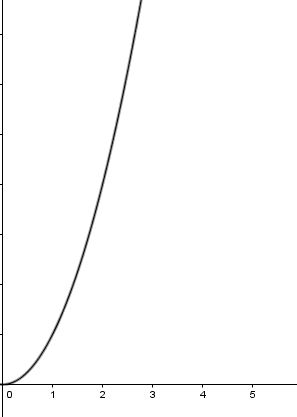
Mentre, per questi studenti, non sono direttamente proporzionali le grandezze rappresentate in figura.
Alcuni studenti affermano che:
due grandezze sono direttamente proporzionali se al raddoppiare di una raddoppia anche l’altra
Le due affermazioni sono evidentemente in accordo per alcuni casi, ma per altri (una retta non passante per l’origine, una retta con coefficiente angolare negativo) le affermazioni sono in disaccordo.
Appare chiaro, subito, che solo una delle due affermazioni potrebbe essere una buona definizione di proporzionalità diretta, ma entrambe creano delle misconcezioni (ad esempio se una grandezza vale 4 e l’altra -1, se una diventa 8 e l’altra -2, le due grandezze sono raddoppiate, ma non tutti riconosco questa cosa per numeri negativi, in quanto il raddoppiare “significa aumentare in senso assoluto”)
Dopo una discussione durata circa 20 minuti, discutendo su esempi concreti, si conclude che:
Due grandezze sono direttamente proporzionali se il rapporto tra la variazione di una e dell’altra si maniene costante.
Questa definizione , concludiamo, è da preferire con quella classica: il rapporto tra le due grandezze si mantiene costante, poichèrisolve il problema puntuale dello zero. Inoltre permette di riconoscere come direttamente proporzionali tutte le grandezze rappresentate da una retta, anche non passante per l’origine ( traslazione, posizione iniziale)
Utilizzando tale definizione è stato chiesto agli alunni di rappresentare e modellizare tre fenomenoifisico dove , per ipotesi, due grandezze sono direttamente proporzionali tra loro ed , in una seconda fase, inversamente proporzionali.
Gli studenti sono stati divisi in gruppi da 4 (o da 3) e ad ognuno è stato assegnato un ruolo (Esperto digitale, Amico critico, Relatore, Segretario), mentre ognuno poteva raccogliere dati ed effettuare l’esperimento.
1 ora è stata dedicata al design dell’esperimento: gli studenti con carta e penna o pc /tablet/smartphone sono stati lasciati liberi di organizzare gli esperimenti , di organizzare il setting sperimentale, di descrivere le ipotesi teoriche che li hanno condotti all’esperimento.
Nella fase sperimentale gli studenti non hanno solo raccolto i dati, ma hanno rappresentato il fenomeno graficamente, deducendo un possibile modello fisico che spiegasse il fenomeno stesso. Nella fase finale il modello sperimentale è stato raccordato con quello teorico e sono state suggerite eventuali previsioni future.
Di seguito vengono allegate 3 relazioni significative sulla proporzionalità diretta ed in una successivo lavoro, sulla proporzionalità inversa.
In tutte le fasi del lavoro, il docente ha avuto il ruolo di mediatore semantico, di risolvere le situazioni di stallo, di suggerire possibili esperimenti, senza forzare.
Per tutte le attività i gruppi potevano fare 5 minuti di pausa , che avveniva in classe e i relatori potevano stabilire un incontro tra gli altri esperti o relatori di gruppi diversi, in modo da suggerire e risolvere possibili difficoltà.
L’analisi dei dati è avvenuta con un foglio elettronico (sconosciuto alla maggior parte degli alunni).
Gli esperimenti proposti dagli studenti nei file allegati sono:
Relazione tra altezza di no smartphone da terra e pressione
Relazione tra massa di acqua e tempo di ebollizione
Relazione tra altezza di un oggetto e la sua ombra (a parità di angolo di inclinazione della luce incidente)
Relazione tra battito cardiaco e velocità
Relazione tra massa ed allungamento di un materiale elastico
Relazione tra volume di acqua ed altezza di un recipiente (di Superficie di base fissata)
Relazione tra spazio percorso e tempo impiegato di un verme in moto
I lavori sono riportati così come sono arrivati al sottoscritto.
Dai lavori emerge che quasi tutti i gruppi sanno riconoscere la proporzionalità diretta nei fenomeni naturali, ma non sempre sanno individuare il modello fisico o matematico che lo rappresenta. Riconosco la proporzionalità diretta se hanno un facilitatore iconico e on sempre la verificano in base alla relazione matematica tra due grandezze.
In molti casi gli studenti hanno utilizzato lo smartphone per effettuare misure fisiche utilizzando i sensori ambientali e software suggeriti dal docente. L'utilizzo dello smartphone è avvenuto in maniera naturale
Il lavoro di gruppo e l’autonomia di lavoro sviluppa sicuramente competenze sociali e relazionali ed in tutti gruppi è buona l’analisi dei dati.
Tali attività sono state proposte nel primo mese di scuola, ed anche se i ragazzi non conoscono le leggi fisiche, hanno lo scopo di motivare gli studenti allo studio della fisica, a mostrare come essa non sia un disciplina astratta, presente solo nei libri, ma è presente in tantissimi fenomeni naturali.
Si sottolinea come l’originalità e la fantasia degli studenti si è spesso cozzata con un non accordo tra i fenomeni studiati (in totale sono arrivati ben 21 esperimenti originali su presunta proporzionalità diretta).
Per le altre lezioni visita la pagina dedicata: Didattica Fisica
Per qualsiasi dubbio o suggerimenti scrivetemi ad Questo indirizzo email è protetto dagli spambots. È necessario abilitare JavaScript per vederlo.